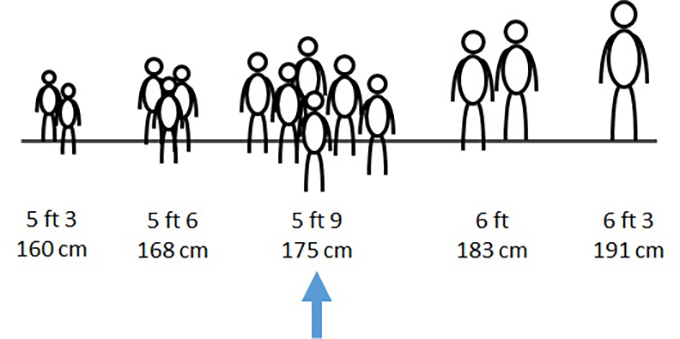
When analyzing a set of data, one of the first steps many people take is to compute an average. You might compare your height against the average height of people where you live, or brag about your favorite baseball player’s batting average. But while the average can help you study a dataset, it has important limitations.
Uses of the average that ignore these limitations have led to serious issues, such as discrimination, injury and even life-threatening accidents.
For example, the U.S. Air Force used to design its planes for “the average man,” but abandoned the practice when pilots couldn’t control their aircraft. The average has many uses, but it doesn’t tell you anything about the variability in a dataset.
I am a discipline-specific education researcher, meaning I study how people learn, with a focus on engineering. My research includes study of how engineers use averages in their work.
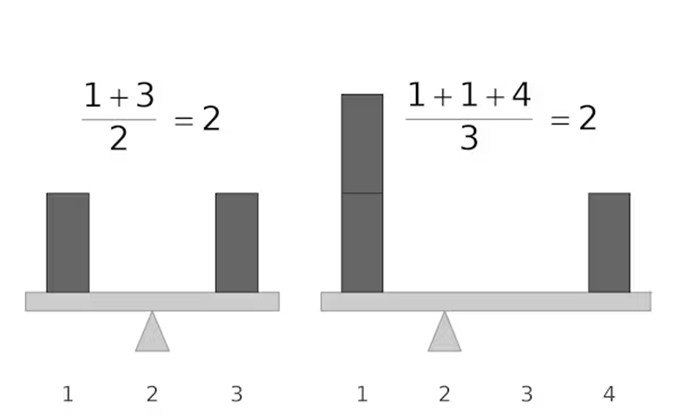
If each data point is a weight on a seesaw, with a position determined by its value, the average is the point where the seesaw will exactly balance. If there are multiple data points with the same value, you can imagine stacking weights at the same point. Zachary del Rosario
Using the average to summarize data
The average has been around for a long time, with its use documented as early as the ninth or eighth century BCE. In an early instance, the Greek poet Homer estimated the number of soldiers on ships by taking an average.
Early astronomers wanted to predict future locations of stars. But to make these predictions, they first needed accurate measurements of the stars’ current positions. Multiple astronomers would take position measurements independently, but they often arrived at different values. Since a star has just one true position, these discrepancies were a problem.
Galileo in 1632 was the first to push for a systematic approach to address these measurement differences. His analysis was the beginning of error theory. Error theory helps scientists reduce uncertainty in their measurements.
Error theory and the average
Under error theory, researchers interpret a set of measurements as falling around a true value that is corrupted by error. In astronomy, a star has a true location, but early astronomers may have had unsteady hands, blurry telescope images and bad weather – all sources of error.
To deal with error, researchers often assume that measurements are unbiased. In statistics, this means they evenly distribute around a central value. Unbiased measurements still have error, but they can be combined to better estimate the true value.
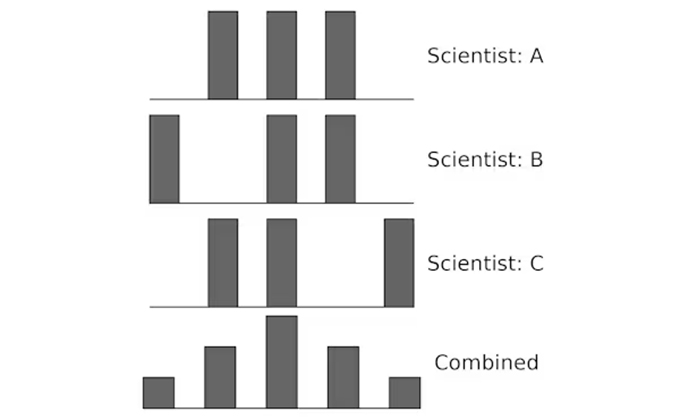
Small numbers of measurements seem random, but a large set of unbiased measurements will distribute evenly around the average. Zachary del Rosario
Say three scientists have each taken three measurements. Viewed separately, their measurements may seem random, but when unbiased measurements are put together, they evenly distribute around a middle value: the average.
When measurements are unbiased, the average will tend to sit in the middle of all measurements. In fact, we can show mathematically that the average is closest to all possible measurements. For this reason, the average is an excellent tool for dealing with measurement errors.
Statistical thinking
Error theory was, in its time, considered revolutionary. Other scientists admired the precision of astronomy and sought to bring the same approach to their disciplines. The 19th century scientist Adolphe Quetelet applied ideas from error theory to study humans and introduced the idea of taking averages of human heights and weights.
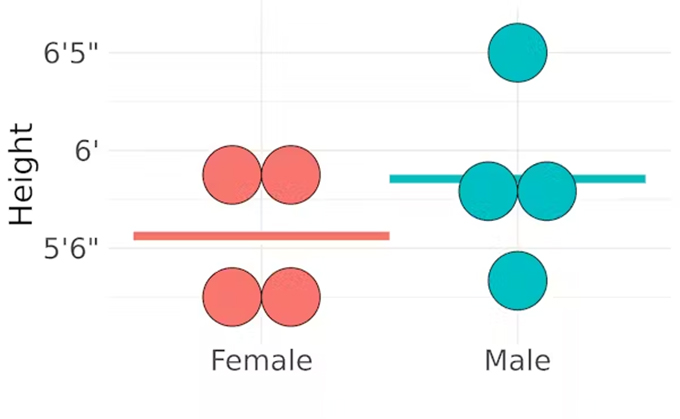
An example dataset of female and male heights. Dots are individuals, while the horizontal lines are the averages. The men are taller on average, but some of the females are taller than some of the males. The average does not tell you everything, particularly when there is real variation. Zachary del Rosario
The average helps make comparisons across groups. For instance, taking averages from a dataset of male and female heights can show that the males in the dataset are taller – on average – than the females. However, the average does not tell us everything. In the same dataset, we could likely find individual females who are taller than individual males.
So, you can’t consider only the average. You should also consider the spread of values by thinking statistically. Statistical thinking is defined as thinking carefully about variation – or the tendency of measured values to be different.
For example, different astronomers taking measurements of the same star and recording different positions is one example of variation. The astronomers had to think carefully about where their variation came from. Since a star has one true position, they could safely assume their variation was due to error.
Taking the average of measurements makes sense when variation comes from sources of error. But researchers have to be careful when interpreting the average when there is real variation. For instance, in the height example, individual females can be taller than individual males, even if men are taller on average. Focusing on the average alone neglects variation, which has caused serious issues.
Quetelet did not just take the practice of computing averages from error theory. He also took the assumption of a single true value. He elevated an ideal of “the average man” and suggested that human variability was fundamentally error – that is, not ideal. To Quetelet, there’s something wrong with you if you’re not exactly average height.
Researchers who study social norms note that Quetelet’s ideas about “the average man” contributed the modern meaning of the word “normal” – normal height, as well as normal behavior.
These ideas have been used by some, such as early statisticians, to divide populations in two: people who are in some way superior and those who are inferior.
For instance, the eugenics movement – a despicable effort to prevent “inferior” people from having children – traces its thinking to these ideas about “normal” people.
While Quetelet’s idea of variation as error supports practices of discrimination, Quetelet-like uses of the average also have direct connections to modern engineering failures.
Failures of the average
In the 1950s, the U.S. Air Force designed its aircraft for “the average man.” It assumed that a plane designed for an average height, average arm length and the average along several other key dimensions would work for most pilots.
This decision contributed to as many as 17 pilots crashing in a single day. While “the average man” could operate the aircraft perfectly, real variation got in the way. A shorter pilot would have trouble seeing, while a pilot with longer arms and legs would have to squish themselves to fit.
While the Air Force assumed most of its pilots would be close to average along all key dimensions, it found that out of 4,063 pilots, zero were average.
The Air Force solved the problem by designing for variation – it designed adjustable seats to account for the real variation among pilots.
While adjustable seats might seem obvious now, this “average man” thinking still causes problems today. In the U.S., women experience about 50% higher odds of severe injury in automobile accidents.
The Government Accountability Office blames this disparity on crash-test practices, where female passengers are crudely represented using a scaled version of a male dummy, much like the Air Force’s “average man.” The first female crash-test dummy was introduced in 2022 and has yet to be adopted in the U.S.
The average is useful, but it has limitations. For estimating true values or making comparisons across groups, the average is powerful. However, for individuals who exhibit real variability, the average simply doesn’t mean that much.
Author Bio: Zachary del Rosario is Assistant Professor of Engineering at the Olin College of Engineering
