“This immense book that always stands open before our eyes, I mean the Universe […] is written in the language of mathematics  ,” wrote Galileo, the founding figure of modern science. The aim of this article is to question this tenacious presupposition in science, according to which the notions of reality, language and truth maintain robust and natural links, to the point of merging. We will put it to the test of a mathematical theorem that, from this point of view, appears very paradoxical .

A century-old paradox

Let’s start with this theorem, whose centenary is celebrated in 2024, known as the Banach-Tarski paradox, their two authors. This statement is accompanied by an irrefutable proof, according to the rigorous standards of mathematics, where the truth is defined very precisely. It is therefore above all not a paradox, but rather a truth, the very one that will concern us below. This theorem states:

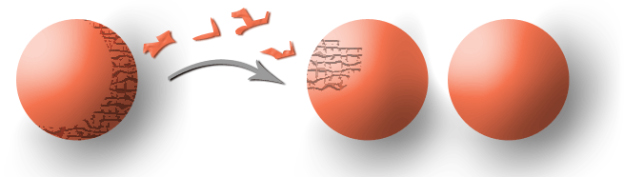
“A ball can be cut into a finite number of parts and rearranged to form two balls identical to the first.”

A wooden ball can be cut and reconstructed into two balls identical to the first, according to the Banach-Tarski theorem. Georges Comte/Université Savoie Mont Blanc , Provided by the author

If he were speaking to us about an everyday experience, this statement would mean that one can cut an orange into carefully chosen pieces and reassemble them (without deforming them) into two oranges identical to the first (without a hole). Then repeat the operation to, from a single orange, obtain as many as one wants. A variant of this theorem is:

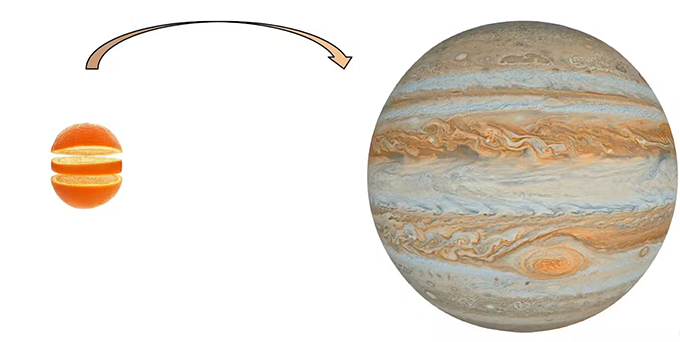
“A given ball can be cut into a finite number of parts and rearranged to form a ball of radius as large as desired.”

An equivalent formulation of the theorem allows us to assert that we can cut a ball and reconstruct it into a larger copy. Georges Comte/Université Savoie Mont Blanc , Provided by the author

We could thus reassemble the pieces of an orange to reconstitute one the size of Jupiter.

A false paradox

The paradox comes from the fact that this statement does not conform to the stubborn experience of reality, where we intuitively assign to every object a volume for which the whole is the sum of its parts. On the other hand, each piece of the division is practically unrealizable, because it is made up of an infinite number of points, while the total number of particles in the universe is finite.

Finally, this statement cannot be proven without accepting a premise called the axiom of choice , so that its truth does not come from a natural principle but from the adoption of a rule of the language game. Here is the logical key to the false paradox: from this axiom flow the pieces of the theorem, for which the objection of the invariance of volume cannot be invoked, because quite simply no mathematical notion of volume can be applied to them.

But an embarrassing false paradox

The great interest of this theorem comes from the fact that the paradox persists, even after having been technically clarified. To understand this difficulty, of a psychological nature, one must delve a little into the history of ideas.

Sciences, such as physics, which study natural phenomena supposed to follow immutable rules, establish mathematical laws with three virtues. First, conciseness, which allows the effective dissemination of knowledge, universally open to scientific controversy. Then the prediction of the course of a phenomenon. Finally, a proven fertility: new, unintuitive concepts appear at the limits of the laws. Black holes or certain elementary particles were thus first predicted by equations.

Under the effect of this mathematization of the natural sciences, it is accepted that this “Nature” is expressed in mathematical language. Even more remarkable is the reciprocal paradigm on which every researcher lives more or less consciously, according to which the mathematical interrogation of nature must reveal its secrets one after the other, and offer the shadowless panorama of reality. The physicist Eugen Wigner calls this faith “the unreasonable effectiveness of mathematics in the natural sciences”.

This belief has the undeniable success of the mathematization of the natural sciences, since airplanes fly, as the laws of aerodynamics predicted. To this must be added a powerful psychological spring: the idea that the whole truth of reality emerges in (mathematical) language is seductive. Scientific progress, in an irrepressible unfolding leaving nothing by the wayside of knowledge, would thus end up exhausting this truth. Everything would be just a matter of patience.

Reality, language and truth: a distant belief

Everything seems to happen as if reality, truth as a concept, that is to say the idea that one can assign a value to any discourse on nature (true or false) and that in return each phenomenon is assignable to a law, and finally language well calibrated by grammar and logic, occupied the three vertices of an immutable conceptual triangle, sometimes confused, and that in the absence of one of them the other two would disappear.

This conception, reactivated in the Renaissance, can be traced back at least to Plato of the classical Greek era, who postulated the existence, certain but overhanging, of a reality established in the inaccessible world of Ideas, of which only the dark and crude projections are shown (each representation here below of a circle is an imperfect image of the Idea of ​​the circle). This distant existence of reality would further oblige us to journey towards it, because guided by the principle of truth, we could be led to the heaven of Ideas. It was Euclid (3rd ^century  BC) who under this regime established mathematics as a hypothetico-deductive model science: from a minimal number of axioms, logical reasoning, from truth to truth, raises us to the highest properties of geometry and numbers.

Previously, the distant Mesopotamian civilization had not formalized its relationship to reality, language, and truth in this way, and even less had it held these three together. Their texts report a performative, divinatory use of language (reality conforms to what is said about it, and not the other way around). As for Mesopotamian mathematics, it is not concerned with a system of axioms or the generalization of formulas, which never go beyond practical problems. A civilization for which, in the words of Richard Powers in his novel Siderations  :

“The world is an experiment in the invention of validity, and conviction is its only proof.”

An illusion denied by mathematics itself

It was Nietzsche who first became concerned about our Platonic faith in a holy trinity of reality-language-truth, where each statement takes on the marvelous character of a veil lifted over the supposed truth of the world. Which in turn gives a blinding, and according to him pathological, creative appearance to (mathematical) language. He sums it up thus in Twilight of the Idols  :

“I fear that we will never get rid of God, since we still believe in grammar.”

Since under this regime of truth the sciences of the real develop in an apparently satisfactory manner, one expects that the directions taken by mathematics itself, as a model science, will specify even more clearly this shadowless outline of the truth of the real. But a theorem like that of Banach-Tarski seems on the contrary to ruin these imaginary links between the real, language and truth.

Reality and mathematics freed from their bonds

What can we conclude? This example of an unreal mathematical truth attests to the autonomy of mathematics, which unfolds outside of sensible reality, in a language concerned only with its internal truth, based on conscious choices of rules. While the paradox felt is only the effect of an illusion, that of the imaginary links reality-language-truth described above. Mathematics is far from resembling what Wittgenstein designates in his Philosophical Remarks as a “phenomenological language, grammar of the facts on which physics constructs its theories”.

This in turn questions the idea of ​​a Nature previously written in mathematical language: when the mathematical arrow reaches a truth, it can be unreal. But we must equally consider that its trajectory ignores an inaccessible set of phenomena, because they are forever untranslatable in its language, and whose potentially immense configuration draws the unthinkable edges of expressible knowledge. This is the inverse postulate of Platonism.

Breaking with the reassuring opinion of a mathematical science gradually translating the whole truth of reality probably does not help to produce more knowledge, but it puts us in a much better position to think validly about both reality and knowledge.

Author Bio: Georges Comte is a University Professor – Mathematics at Savoie Mont Blanc University